1. 문제 설명

문제 링크

< M:N >이란 달력이 있는데, (x,y) -> (1,1) , (2,2) 가다가 x가 M을 넘거나, y가 N을 넘으면 다시 1로 돌아온다.
예제에 설명되어 있는 대로, <10,12> 일때, 13번째 년도는 <3,1>이 된다. <10,10> , <1,11>, <2,12>, <3,1> 순으로 온다.

문제에서 M,N,x,y를 줄 때, <M,N> 달력에서 <x,y>가 몇 번째 년도인지 구하라.

2. 접근 방식

이것도 도저히 생각이 안나서 다른 사람 풀이 봤다. (요즘 왜 이렇게 풀이가 생각이 안나지? 더 열심히 해야겠다.)
KEY WORD: 유클리드 호제법, LCM과 GCD의 관계

먼저 <1,1> ~ <M,N>까지 순서대로 번호를 매긴다고 해보자. 이때 우리가 구해야하는 <x,y>는 K번째 수라고 해보자.
x는 K를 M으로 나누었을 때의 나머지이고, y는 K를 N으로 나누었을 때 나머지 이다.

<10,12>에서 <3,9>는 33번째 수인데, 33%10 = 3, 33%12 = 9 임을 알 수 있다.
식으로 나타내보겠다.

K = M * q + x 
K = N * q` + y

여기서 M이 고정되어 있더라도 x가 나오는 K는 여러가지일 수 있다. 그렇다고 1부터 모든 수를 K에 대입하여 구한다면 시간 초과가 난다. 어떻게 해야할까?

나머지가 x가 나오는 K가 N으로 나누었을 때 y가 나온다면 우리가 찾는 수이다.
나머지가 x가 나오는 수들을 후보군으로 두고 문제를 풀면 되므로, q를 올려서 자격이 없는 숫자들은 건너뛴다.

문제의 예시로 예를 들어보자.
우리는 <10,12>에서 <3,9>가 몇번째 수인지 찾아내야 한다.
먼저 q = 0일때, 생각해보면, K = 0+3 이다. 이것을 N인 12로 나누면, <3,3>이 나온다. 따라서 탈락
두 번째, q = 1 일때, K = 13이다. 이것을 12로 나누면 1 즉 <3,1>이 나온다. 탈락
세 번째, q = 2 일때, K = 23이다. 이것을 12로 나누면, <3,11>이 나온다. 탈락
네 번째, q = 3 일때, K = 33이다. 이것을 12로 나누면 <3,9>가 나온다. 정답!

※주의: 범위 정하기

하지만 문제에서는 절대 카잉 달력에 나올 수 없는 숫자를 입력을 줄 수도 있다. 이때, 범위를 정해놓고 계산에 임하지 않으면 무한 루프에 빠질 것이다. 어디까지 계산 해야할까? 카잉달력은 Max값인 <M,N> 에 도달하면 종말을 맞이하고 끝난다.
그러면 <M,N>은 과연 몇 번째 수인가?

<M,N>의 순번은 M과 N의 최소공배수이다.
왜냐하면, 두 수의 순환이 같아지는 순간이 바로 끝이기 때문이다. <7,5>면 두 수가 같이 원점에 가는 순간은 35번째 순간이다.

최소 공배수 어케 구함?
여기서 수학적 지식이 없으면 헤맨다. 나도 헤매었다.

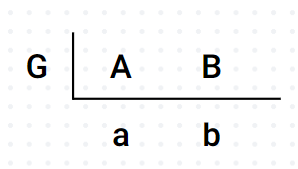
두 수 A,B의 최대공약수를 G라고 할 때, 나누면 다음과 같이 될 것이다. a와 b는 서로소이다.

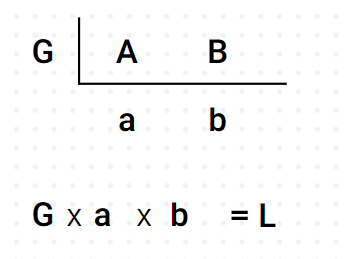
이때, 최대공약수 x a x b = 최소공배수 이다.
그럼 A,B를 곱해보자. AxB= (Ga) x (Gb) 와 같다. 이것을 G로 나누면?

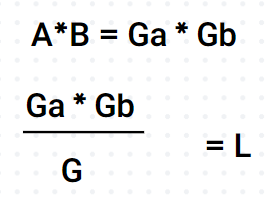
최소공배수가 나온다. 따라서 두수의 곱 / 최대공약수 = 최소 공배수라는 관계가 나온다. 이를 이용해 문제를 풀면 된다.

그럼 최대공약수는 어케 구함?
이건 유클리드 호제법을 쓰면 된다. 유클리드 호제법은 간단히 말해서
A = Bq + R 일때, A와 B의 최대공약수는 B와 R의 최대공약수와 같다는 것이다. 이것을 이용해서 연속적으로 나누다 보면 어느 순간
B = Rq + 0 의 순간이 온다. 이러면 R는 B의 약수이고, B와 R의 최대공약수는 R 자신이 된다. 그렇다면 A,B의 최대공약수도 유클리드 호제법에 따라 R이 된다.

한 줄 요약

따라서 이를 이용해 M과 N의 최대공약수 -> 그걸로 둘 사이의 최소공배수 구함 -> M*q 가 최소공배수를 넘지 않을 때까지 반복으로 범위를 정해서 풀면 된다.

3. 코드 분석

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int test_case = Integer.parseInt(br.readLine());
        for (int t = 0; t < test_case; t++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int M = Integer.parseInt(st.nextToken());
            int N = Integer.parseInt(st.nextToken());
            int x = Integer.parseInt(st.nextToken());
            int y = Integer.parseInt(st.nextToken());
            // 1. 최소 공배수 구하기 -> 최소 공배수를 넘어서 계속 값을 유추하고 있으면 유효하지 않은 수임으로 -1 출력
            int lcm = M>N? (M*N/gcd(M,N)) : (M*N/gcd(N,M));
            // 2.
            int ans = -1;
            int n = 0;
            while (n*M < lcm) {
                if((n*M+x-y)%N == 0) {
                    ans = n*M+x;
                    break;
                }
                else  n++;
            }
            System.out.println(ans);
        }
    }
    public static int  gcd (int A, int B) {
        if(A%B == 0) return B;
        else return gcd(B, A%B);
    }
}