1. 문제 설명
뭔놈의 극장이 티켓을 샀는데, 양 옆으로 옮겨 앉을 수 있음...
예를 들어 3번 좌석을 산 사람은 4번 좌석에 앉아도 되고, 2번 좌석에 앉아도 됨.
하지만 3번 좌석을 산 사람이 양 옆 이외의 좌석에는 못 앉음. 예를 들어 7번 좌석이나 1번 좌석으로 이동은 불가.
또, VIP석이라는 개념이 있음. 이름이랑 맞지 않게 이거 산 사람은 그냥 그 자리 앉아야함.
예를 들어 7번 좌석이 VIP석이면 7번 산 사람은 7번에 무조건 앉아야함.
N번까지의 좌석이 있고, 만석일 때, 사람들끼리 자리를 바꿔 앉을 수 있는 경우의 수를 구하라.
2. 접근 방식
도저히 못 풀겠어서 다른 사람 풀이를 봤다.KEY WORD : DP
(1) 기본 원리
패턴이 안 보이면, 무작정 가짓수를 적어서 패턴을 생각해봐야 한다는 것을 깨달았다. 해당 문제의 패턴은 다음과 같다.
(일단 고정석은 생각하지 말자.)
좌석이 1 개일 때, 앉을 수 있는 경우의 수는 1가지 이다.
좌석이 2개 일 때, 티켓 1번과 티켓 2번이 서로 자리를 바꿔 앉을 수 있다. (1,2), (2,1) 따라서 경우의 수는 2가지다.
좌석이 3개 일 때, (1,2,3), (1,3,2), (2,1,3)으로 3가지이다.
좌석이 4개 일 때, (1,2,3,4), (2,1,3,4), (1,3,2,4), (1,2,4,3),(2,1,4,3) 으로 5 가지 이다.
좌석이 5개 일 때, (1,2,3,4,5), (2,1,3,4,5), (1,3,2,4,5), (1,2,4,3,5), (1,2,3,5,4),(2,1,4,3,5),(2,1,3,5,4),(1,3,2,5,4)로 8가지이다.
피보나치 수열과 거의 유사한 형태임을 알 수 있다. 따라서 DP 점화식은(i>2 일 때) dp[i] = dp[i-1] + dp[i-2]이다.
(2) 고정석을 산정해보자.
이건 쉽다. 고정석은 어짜피 고정 되어있어서 경우의 수를 만들지 못한다. 또한 양 옆의 자리만 바꿀 수 있으니,고정석이 생기면, 고정석 이후부터 다시 피보나치 수열 시작이다.
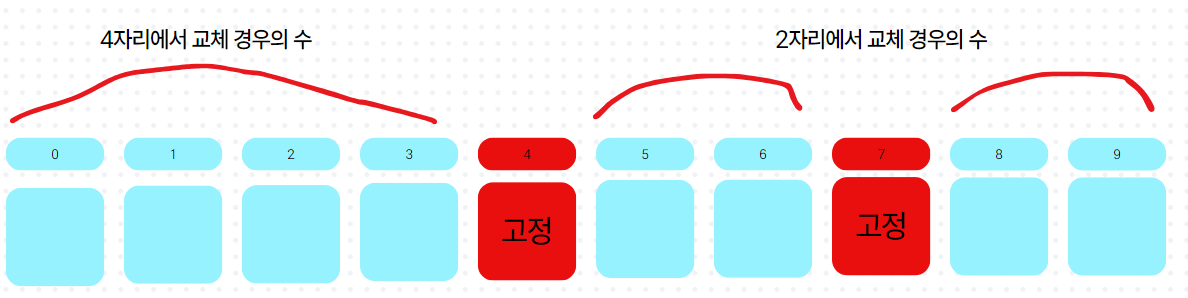
따라서 풀 수 있는 방법은 2가지이다.
- 위의 생각한 그대로 고정석 나올 때마다 dp 새로 세기
- dp는 일단 N개에 관해서 전부 구해놓고, 고정석을 만날 때마다 가용 범위 만큼 구해서 쓰기
1번은 직관적이니까 넘어가고, 2번의 경우가 무엇을 뜻하는지 알아보자
일단 문제의 예시처럼 N=9라고 할때, dp를 다 구하면 다음과 같다.
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55]4번이 고정석이라면 무슨 소리일까? 1~3번 3개의 자리에서만 자리를 바꾸는 경우의 수를 구하면 된다. 따라서 답은 3이다.
7번에서 고정석을 또 만나면 5,6번 자리 바꾸기만 생각하면 된다. 따라서 답은 2이다.
마지막도 8,9 두 자리를 바꾸면 되니까 답은 2이다.
각 자리를 바꾸는 경우는 동시에 일어나므로 곱해야 한다. 따라서 3x2x2 해서 정답은 12이다.
3. 코드 분석
1번 풀이
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
int ans = 1;
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int [] dp = new int[N+1];
dp[0] = -1;
int M = Integer.parseInt(br.readLine());
for (int i = 0; i < M; i++) {
int now = Integer.parseInt(br.readLine());
dp[now] = -1;
}
for (int i = 1; i <= N; i++) {
if(dp[i] == -1) continue;
if(dp[i-1] == -1) {dp[i] = 1;}
else if(dp[i-2] == -1) {dp[i] = 2;}
else dp[i] = dp[i-1] + dp[i-2];
if(i+1 > N || dp[i+1] == -1) ans *= dp[i];
}
System.out.println(ans);
}
}2번 풀이
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
if(N == 1) {
System.out.println(1);
return;
}
int [] dp = new int [N+1];
dp[0] = 1;
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i <= N; i++){
dp[i] = dp[i-1] + dp[i-2];
}
int ans = 1;
int vip_recent = 0;
st = new StringTokenizer(br.readLine());
int M = Integer.parseInt(st.nextToken());
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int vip_now = Integer.parseInt(st.nextToken());
ans *= dp[vip_now - vip_recent-1];
vip_recent = vip_now;
}
ans *= dp[N-vip_recent];
System.out.println(ans);
}
}!! 왜 dp[0] = 0이 아니라 1 입니까?
원래 dp[0]는 사용하지 않는 배열 원소이다. 하지만 2번 풀이와 같이 풀면 쓸 때가 있다. 만약 고정석이 9개의 좌석 중 6번 7번에 연달아 있다고 해보자.
만약 7-6-1이므로 dp[0]를 사용해야 하는데, dp[0] = 0 이면 이후, 경우의 수로 뭘 구하든 답이 0이 나온다.
고정석이 연달아 있을 경우, 그 사이 좌석 배치 경우의 수는 딱 그 한가지 이므로 dp[0] = 1 로 해야지 경우의 수를 구하는데 차질이 없다.
4. 성장 하기
두 번째 풀이의 dp[0] = 0 이 아니라 1인 이유를 찾는데 시간이 많이 들었던 것 같다. 질문 게시판에 누군가 올린 질문을 통해 답을 알 수 있었다.






