1. 문제 설명 📌
문제 설명 생략
2. 접근 방식 🗃️
KEY WORD: GREEDY ALGORITHM
Greedy 알고리즘은 매 선택의 순간에 당시 할 수 있는 최선의 선택을 하는 것이 전체 문제에서도 최적의 해를 구하는 것임을 가정하는 알고리즘이다.
여기서는 미사일의 묶음을 끝지점 기준 오름 차순으로 정렬하고, 미사일 묶음의 최대한 끝지점에서 차례대로 요격해 나가면 최소한으로 요격 미사일을 사용하는 것이다. 해당 방법은 다음과 같은 이유로 유효하다.
- 미사일을 만나면 무조건 요격해야 한다. 안하고 지나치는 경우는 없다.
- 따라서 미사일을 만나면 최대한 겹치게 삭제해야 한다.
- 하나의 미사일 묶음 A가 다른 미사일 묶음과 최대한 겹치는 경우는 A의 끝지점에서만 발생한다.
예를 들어보겠다.

다음과 같이 폭격 미사일이 나란히 온다고 가정해보자. 해당 그래프에서 끝지점을 기준으로 차례대로 미사일 묶음을 보겠다. 첫 번째 묶음을 요격하면서 최대한 많은 미사일 묶음을 없애는 경우의 수는 무엇인가?

최대한 뒤에서 요격하는 것이다. 끝지점은 개구간이라 요격에 포함이 안되니 첫 묶음을 1~4 구간이라 쳤을 때 3.9 지점에서 요격했다고 보자. 그럼 이제 2개가 없어진다.
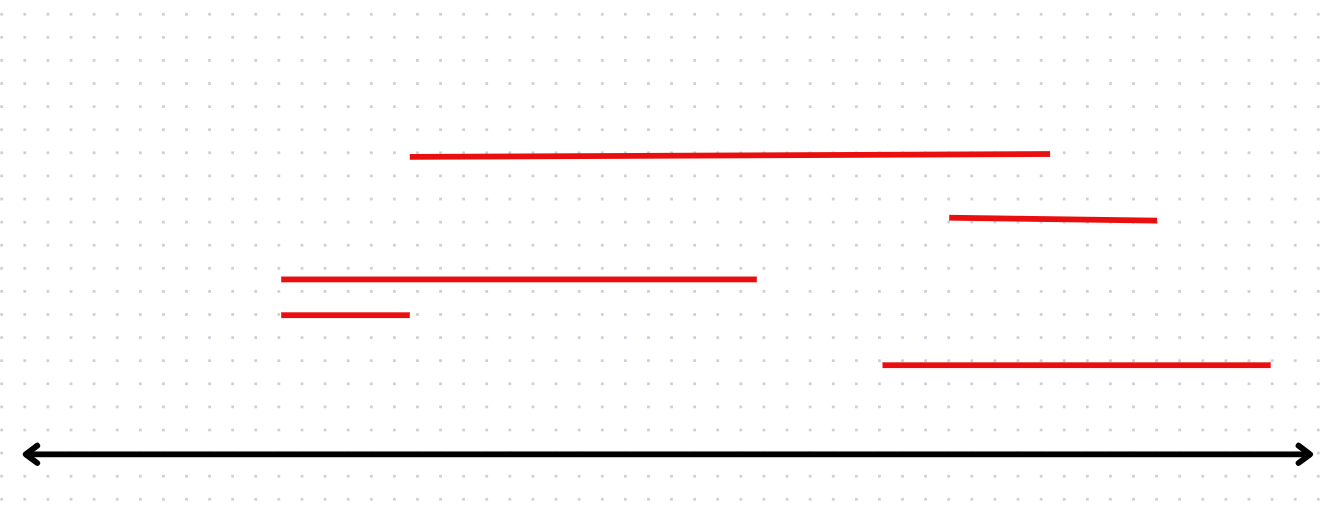
이제 끝지점을 기준으로 제일 우선이 되는 묶음은 제일 짧은 선일 것이다. 해당 묶음을 삭제하면서 최대한 겹치게 삭제하려면 어디서 요격해야 하는가?

해당 묶음의 제일 뒤이다. 해당 묶음을 4~5구간이라 했을 때, 또 4.9에서 요격했다 치자 ^^ 그러면 이제

이렇게 남는다. 이제 제일 긴 묶음이 끝 지점 오름차순 정렬 상 다음으로 조회할 묶음일 것이고, 해당 묶음을 포함해 최대한 많은 묶음을 지우려면

이렇게 지우면 된다.
사실 해당 풀이는 문제의 입출력 예제를 그림으로 구현한 것인데, 문제 속 입출력 예제 설명과 지워지는 양상이 다르다. 그렇다! 문제에서는 Greedy 인 것을 숨기려고 예제에서만 가능한 해를 보여주고 있다!! 이 악마들
(1) 개구간에 요격이 걸치면 해당 미사일 묶음은 제외하는 것에 대한 예외처리는 어떻게 하죠? 🤔
놀랍게도 할 필요 없다. 문제 풀이설명에서 그랬듯이 x=4지점에서 요격했다면 '사실 3.9에서 요격했음 ㅋ'로 대체하면 되기 때문이다. 현 지점 이하의 구간을 가진 미사일 묶음을 모두 지운다로 생각하면 된다.
(2) 시작지점 순으로 정렬하면 안되는 이유?🤔
[[0,4],[1,2],[1,3],[3,4]] 라는 입력을 시작지점 순으로 받으면, 다음과 같다.
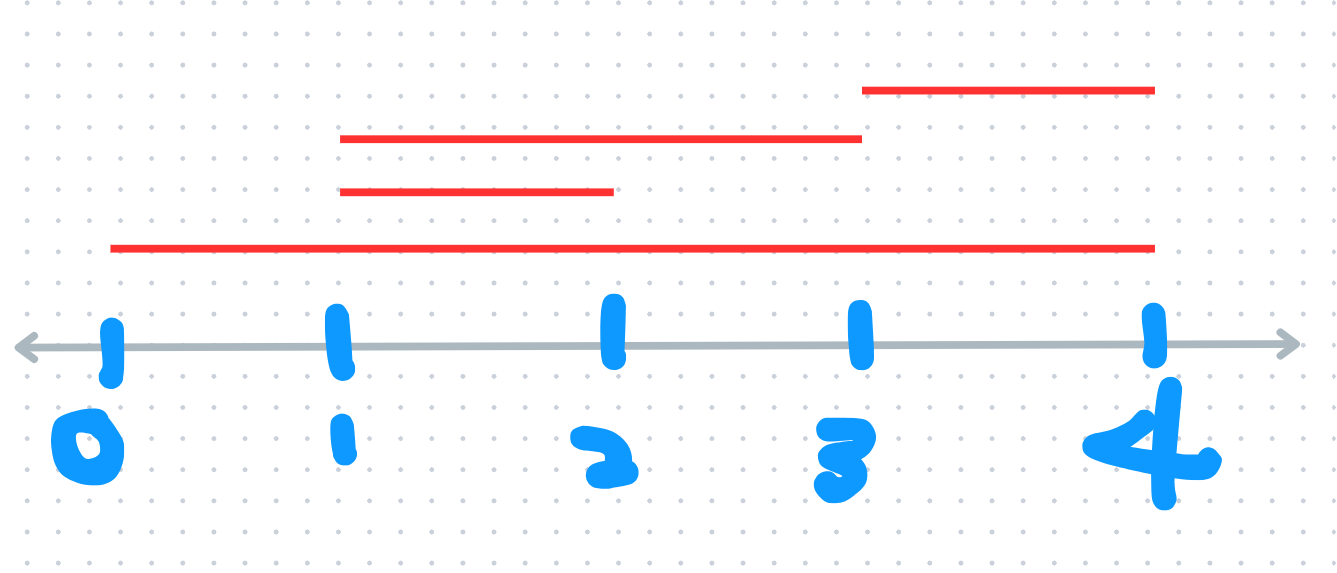
맨 밑의 선분이 정렬 시 가장 앞에 오는 선분이고, 그 다음 순번일수록 위로 올려 배치했다. 이떄 [0,4]의 끝지점에 선분이 그어질 텐데,
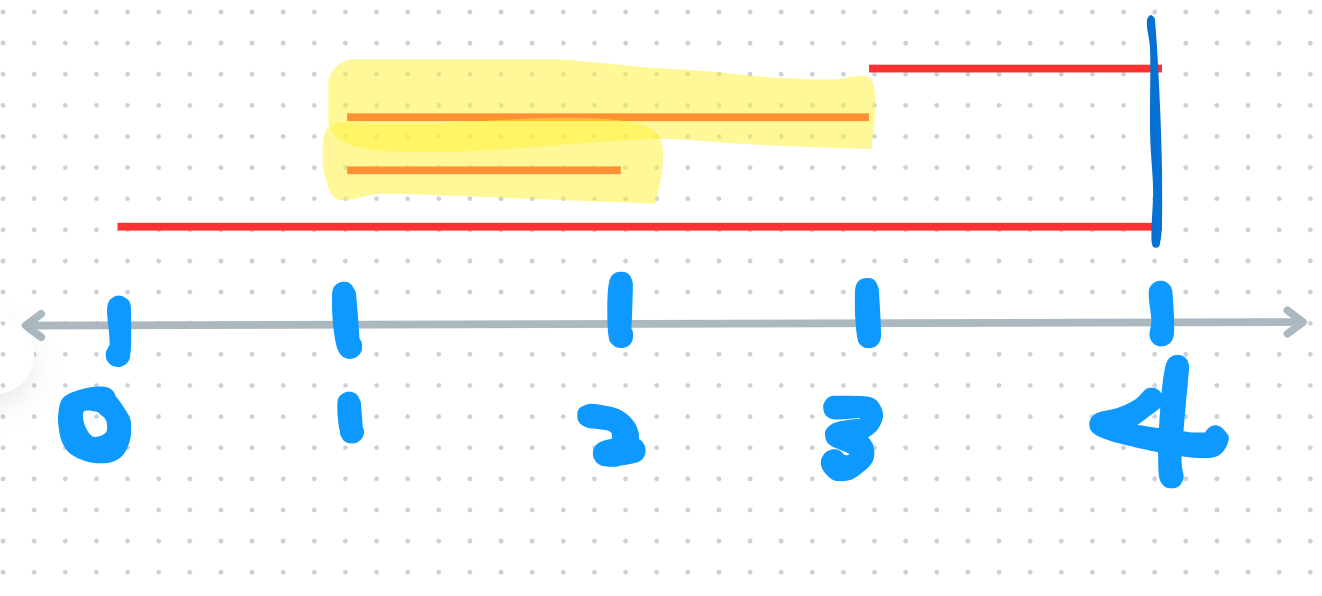
밑줄 친 2개는 확인하지 못하고 넘어간다. 반면 끝 지점 순으로 정렬하면,

이 되고,

지나치는 미사일 모음 없이 모든 미사일을 요격할 수 있게 된다.
즉 시작 지점 순으로 정렬하면, 하나의 선분 안에 여러개의 선분이 포함되면서, 그들이 겹치지 않을 때의 계산이 누락된다.
(3) 풀이 요약
pos= 요격의 x 위치(초기값 0),targets는 끝지점 기반 오름차순 정렬,cnt= 요격 미사일을 쏜 횟수targets에서 하나씩 조회, 만약pos<=targets의 시작 지점이면cnt+1 올리고 pos를 현 조회 중인 targets의 끝지점으로 옮긴다.- 마지막 target값까지 2번을 반복한다.
2번이 의미하는 것이 바로 최대한 뒤에서 쏘는 것이다. 만약 pos > target의 시작지점 라면 현 지점에서 요격 시 같이 없어졌을 것이다. 따라서 이 경우는 요격 미사일 쏜 횟수를 증가시키지 않고 계속 넘어간다. 이후 pos <= target의 시작지점인 값이 나온다면 현 요격 위치에서 없앨 수 있는 미사일 묶음은 다 없앴다는 뜻이므로, 다음 위치로 이동하는 것이다.
3. 코드 소개 🔎
import java.util.*;
class Solution {
public int solution(int[][] targets) {
Arrays.sort(targets, (o1,o2) -> {
if(o1[1] == o2[1]) return o1[0] - o2[0];
return o1[1] - o2[1];
});
int ans = 0;
int pos = 0;
for(int i = 0; i < targets.length; i++){
if(targets[i][0]>= pos){
ans++;
pos = targets[i][1];
}
}
return ans;
}
}4. 배운 것들 🎯
이분 탐색 문제인 줄 알고 이분 탐색으로만 접근하다 보니 문제를 풀지 못했다. 나는 다음과 같이 생각했다.
- 이분 탐색으로 mid값을 정한다.
- mid에서 0.1 더한다.
- 변환된 mid에서 쭉 요격 했을 때, 없어지는 미사일 묶음의 개수를 구한다.
- 현재 구한 묶음의 개수가 이전 묶음 보다 많으면 이분 탐색 진행 아니면 거기서 끝내고 요격 미사일 수 한 개 추가
다음 방식에는 2가지 문제가 있다.
- 이전 묶음보다 현재 없앤 미사일 묶음의 개수가 많았을 때, 어디로 이동할 것인가? 왼쪽으로? 오른쪽으로?
- 이전 묶음보다 작다고 거기서 이분탐색을 종료하면 현재 없앤 미사일 묶음의 개수가 과연 최적의 해인가? 아마 반례가 존재할 듯 하다.
해당 문제는 Greedy인 것만 알면 쉽게 해결하는 문제였는데, 내가 아직 문제에 맞는 알고리즘을 잘 선정하지 못한 것 같다. 이는 문제에 해당하는 알고리즘이 뭔지 아는 체로 문제를 매일 푼 폐단이 아닌가 싶다. 이를 고쳐야 한다.






