다익스트라 알고리즘 구현, 그림으로 쉽게 이해하기

0. 구현 설명에 앞서...

본 포스팅은 'JAVA를 활용해 다익스트라 구현을 어떻게 하는가?'에 대해서 바로 다룰 예정이다. 혹시 이론 공부가 필요하신 분들은 다익스트라 개념 정리 포스트를 한번 읽고 오시길 당부 드린다.

1. 순차 탐색

알고리즘 이론 그대로 코드로 옮긴 구현 방법이다.

• 0️⃣ 시작점에서의 최단 거리 배열 (dist) 만들고 INF로 초기화
• 1️⃣ 현 시점에서 방문하지 않은 노드 중 최소 비용으로 방문할 수 있는 노드(이하 A) 방문
• 2️⃣ 해당 노드와 인접한 노드(이하 B)를 활용해 dist 배열을 최신화 한다.
  • 2️⃣-1) dist[B] > dist[A] + A ➜ B 간선 비용 일 시 dist 배열 최신화
• 3️⃣ 모든 노드를 방문할 때까지 1️⃣,2️⃣ 과정을 반복한다.

(1) 시간 복잡도 분석

노드의 개수: N. 간선의 개수: E 라고 하자.

• 1️⃣ 매번 dist 배열에서 방문하지 않은 노드 중 최소값을 찾는다.
  총 N번의 방문을 할 것인데, 그 때마다 최소 비용 노드를 찾기 위해, dist 배열(N개)를 순회 해야함. : $O(N^{2})$
• 2️⃣ N번의 방문을 하면 결국엔 모든 간선을 다 확인한다는 소리이다. : $O(E)$

따라서 총 $O(N^{2} + E)$의 시간복잡도가 든다.

(2) 구현 코드

import java.io.*;
import java.util.*;

public class 순차탐색_다익스트라 {
    static int [] dist = new int [N];     // N이 변수가 아니라 상수라 치자 
    static boolean [] visited = new boolean [N];
    static ArrayList<Node> [] lists;

     public static void main(String[] args) throws IOException {
         // 배열의 원소가 시작노드, 배열 안의 나열된 값들은 <도착노드, 가중치> 묶음
         lists = new ArrayList [N+1]; 

         for(int i = 1; i < N+1; i++){
             lists[i] = new ArrayList<>();
         }

         // 값 입력 받아서 인접 리스트 채우기 
         // ...
         Dijkstra(1);
    }

    public int 최단거리노드찾기() {
        int min_dist = Integer.MAX_VALUE;
        int min_idx = -1;

        for(int i = 0; i < N; i++){
            if(visited[i]) continue; 
            if(dist[i] < min_dist){
                min_dist = dist[i];
                min_idx = i;
            }
        }
        return min_idx;
    }

    // 시작노드를 인수로 받아서, 해당 노드로부터 모든 노드의 최단 거리를 dist에 입력
    public void Dijkstra(int start) {
        // 1. dist 배열 초기화 
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[start] = 0;
        visited[start] = true;
        // 2. 본 다익스트라 시작 -> 모든 노드 방문할 때까지만 반복하면 됨. 
        for(int i = 0; i < N-1; i++){
            int now_node = 최단거리노드찾기();
            visited[now_node] = true;

            for(int j = 0; j < lists[now_node].size(); i++){
                // 만약 현재까지 j로 가는 최단거리보다 now_node를 거쳐서 j로 가는 최단거리가 더 짧을 경우 갱신
                if(dist[j] > dist[now_node] + lists[now_node].get(j).w){
                    dist[j] = dist[now_node] + lists[now_node].get(j).w;
                }
            }
        }
    }

}

class Node {
    int v; // 도착 노드
    int w; // 도착 노드까지 가는 간선의 가중치 

    public Node(int v, int w) {
        this.v = v;
        this.w = w;
    }   
}

2. 우선순위 큐 활용

dist 배열을 일일히 매번 확인하여 최소 비용 노드 찾기 ➜ 우선순위 큐로 방문 예정인 노드를 dist가 작은 순으로 정렬, 큐의 front 노드를 뽑아서 사용으로 바꾸는 것이다.

• 0️⃣ 정점 번호, 당시 dist[정점 번호]를 가지는 객체, dist 배열과Priority Queue(삽입한 노드의 dist가 작은 순으로 정렬)를 생성한다. 시작점을 PQ에 넣는다.
• 1️⃣ Priority Queue가 빌 때까지 이하 과정을 반복한다.
• 2️⃣ PQ의 front 노드 (이하 A)를 뺴낸다.
• 3️⃣ A.dist(삽입 당시의 최소 비용) != dist[A] 이면 2️⃣으로 돌아간다.
• 4️⃣ 해당 노드와 인접한 노드(이하 B)를 활용해 dist 배열을 최신화 한다.
  • 4️⃣-1) dist[B] > dist[A] + A ➜ B 간선 비용 일 시 dist 배열 최신화

크게 보면, BFS의 queue를 우선순위 큐로 바꾸는 것과 같다.
BFS는 방문 노드의 인접 정점을 빨리 저장한 순으로 방문하는 반면, 우선순위 큐를 쓰면, dist 거리가 최소인 녀석 먼저 방문하는 것이기 때문이다.

(1) 시간복잡도 분석

노드의 개수: N. 간선의 개수: E 라고 하자.

• 1️⃣ 우선순위 큐에서 최소 비용 노드 뽑기 ($O(N log_10 N)$)
  최소 비용 노드를 우선순위 큐에서 뺴는 행위 자체가 $O(N log_10 N)$든다.
• 2️⃣ 모든 간선을 활용하여 우선순위 큐 최신화 ($O(E log_10 N)$)

따라서 총 $O(N log_10 N + E log_10 N)$ 의 시간복잡도가 든다.

(2) 정점을 중복 방문하게 되지 않을까..?

이미 사용한 노드는 다시 사용하지 않는다는 의미의 3️⃣을 과정에 추가 해주었다.

A.dist는 queue에 넣었을 당시, A까지의 최소 비용이다. 근데 이것이 계속 최소값으로 최신화를 거듭한 dist[A]와 다르다면, A.dist는 이미 쓸모 없는 고대의 유물인 셈이다. 따라서 불필요한 계산이 필요 없도록 넘어간다.

(3) 구현 코드

import java.io.*;
import java.util.*;

public class 순차탐색_다익스트라 {
    static int N = 9;
    static int [] dist = new int [N];
    static ArrayList<Vertex> [] lists;

     public static void main(String[] args) throws IOException {
         // 0. initialize
         BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

         lists = new ArrayList [N+1]; 
         Arrays.fill(dist, Integer.MAX_VALUE);
         for(int i = 1; i < N+1; i++){
             lists[i] = new ArrayList<>();
         }

         int edge_cnt = Integer.parseInt(br.readLin());
         for(int i = 0; i < edge_cnt; i++){
             StringTokenizer st = new StringTokenizer(br.readLine());
             int start     = Integer.parseInt(st.nextToken());
             int end     = Integer.parseInt(st.nextToken());
             int cost = Integer.parseInt(st.nextToken());
             lists[start].add(new Vertex(end, cost));
         }

         // 1부터 모든 정점까지의 최단거리를 찾겠다.
         Dijkstra(1);
    }


    // 시작노드를 인수로 받아서, 해당 노드로부터 모든 노드의 최단 거리를 dist에 입력
    public void Dijkstra(int start) {
        PriorityQueue<Vertex> pq = new PriorityQueue<>((o1,o2) -> o1.fast_cost - o2.fast_cost);
        pq.add(new Vertex(start, 0));

        while(!pq.isEmpty()){
            Vertex now = pq.poll();
            if(now.cost != dist[now.idx]) continue;
            for(int i = 0; i < list[now.idx].size(); i++){
                int dest_idx = list[now.idx].get(i).idx;
                int compare_dist = list[now.idx].get(i).weight + dist[now.idx];

                if(compare_dist < dist[dest_idx]){
                    dist[dest_idx] = compare_dist;
                    pq.add(new Vertex(dest_idx, compare_dist));
                }
            }
        }
    }

}

class Vertex {
    int idx;        // 현 정점의 번호
    int cost;     // 시작 정점에서 현 정점까지의 최단 거리 (큐에 집어넣을 당시의 최단거리라서 최신화된 dist 배열과 차이가 날 수 있음)
    public Vertex (int idx, int fast_cost){
        this.idx = idx;
        this.fast_cost = fast_cost;
 }

(3) 예시

1.

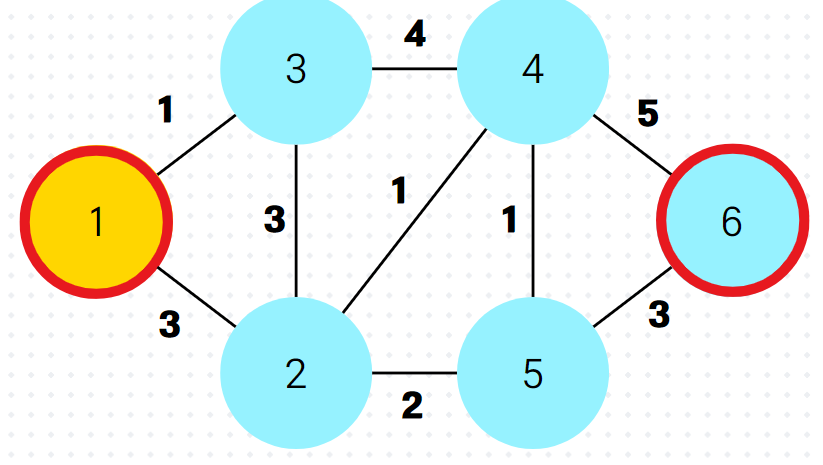
2.

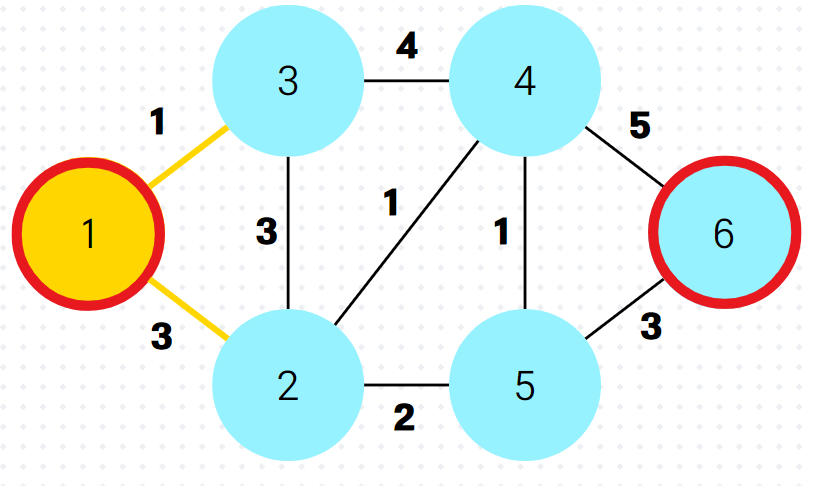
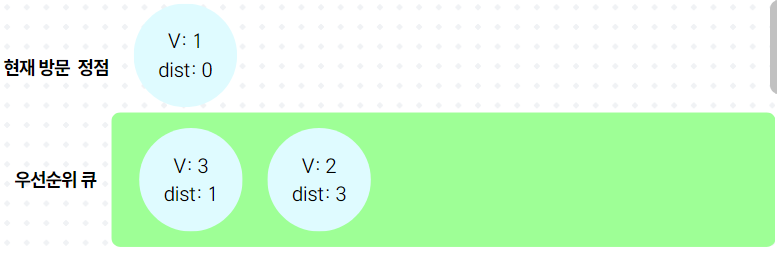
3.

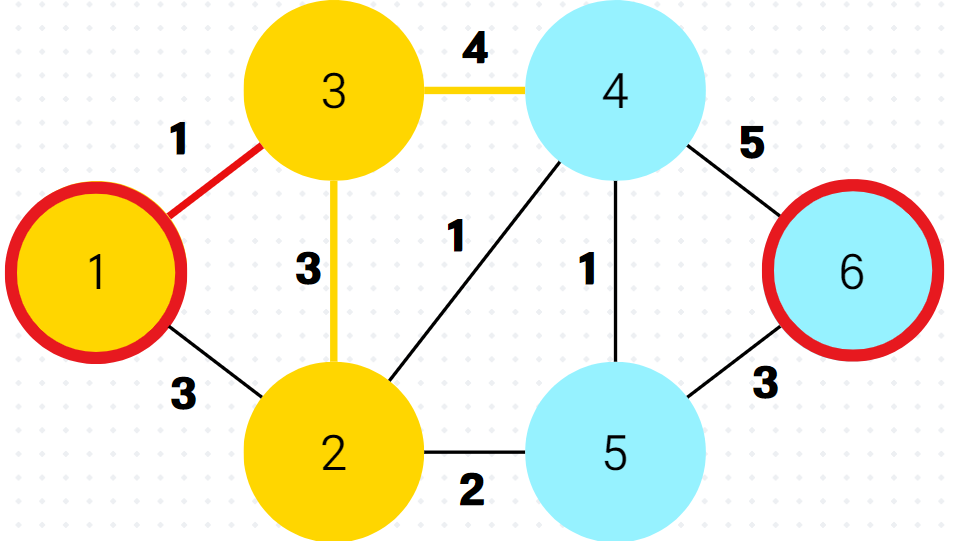
4.

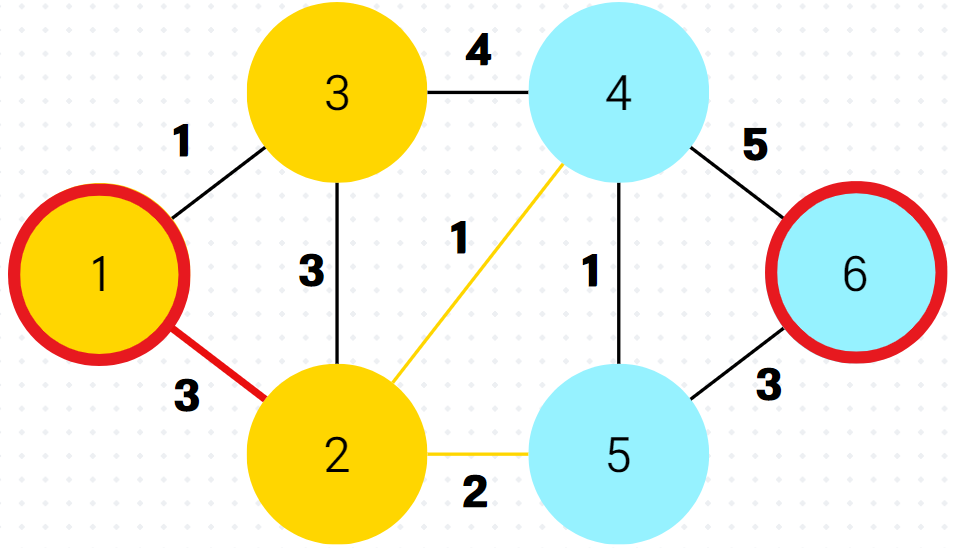
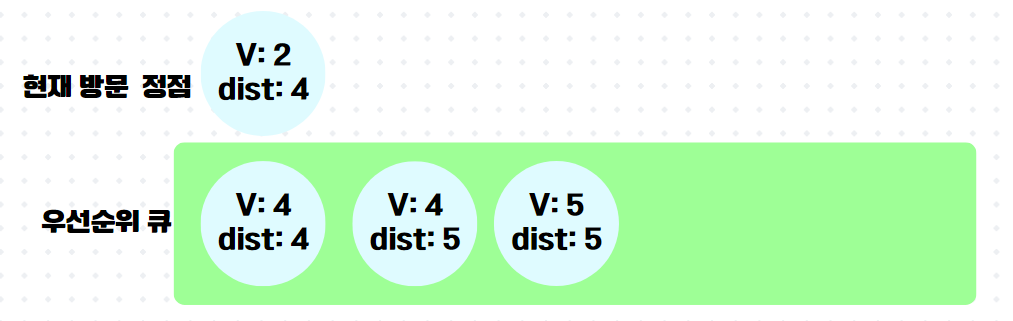
5.

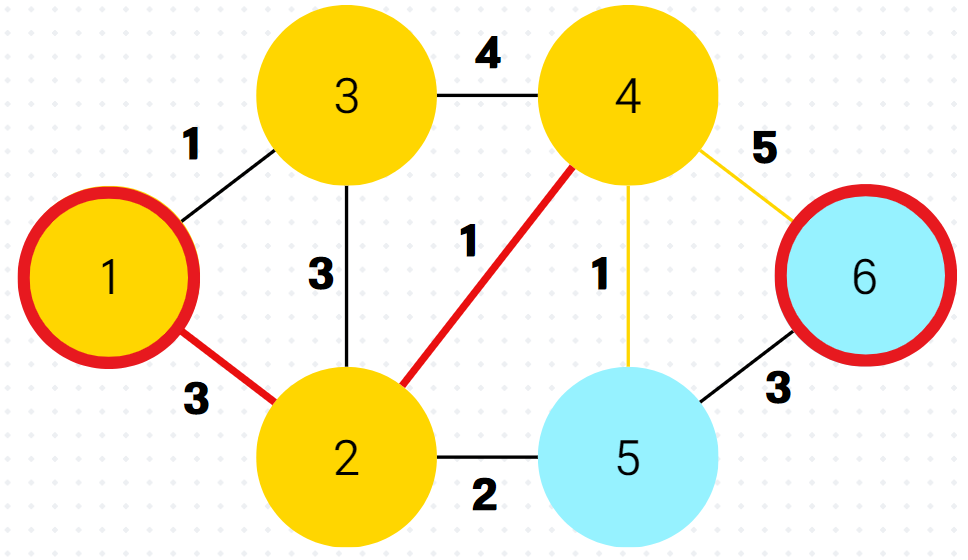
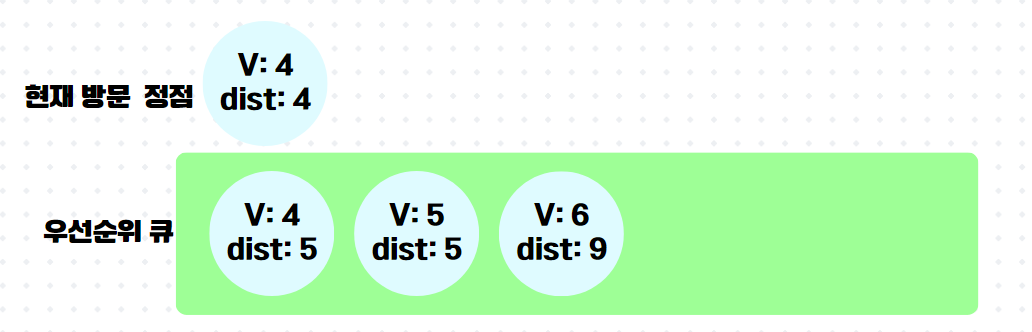
이제 다음이 중요한데, 이미 방문한 정점4가 우선순위 큐의 front에 와있다. 하지만 잘보면 정점4까지의 최단거리라 저장해놓은 것이 5로 이미 최신화된 최단 거리 배열 속 dist[4]의 값보다 크다. 그래서 queue.poll() 하자마자 버린다.

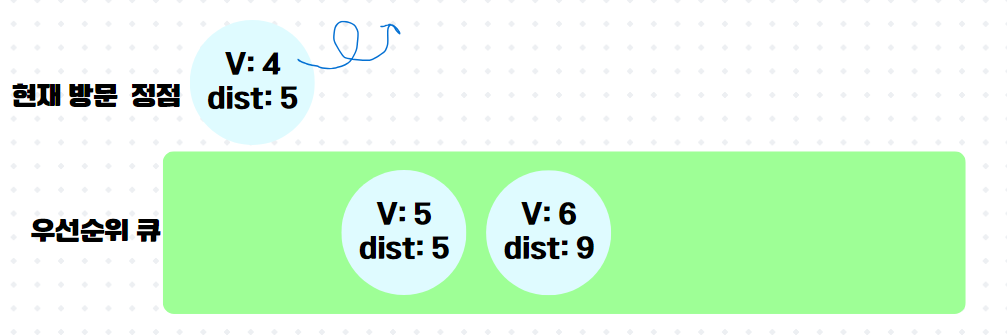
6.

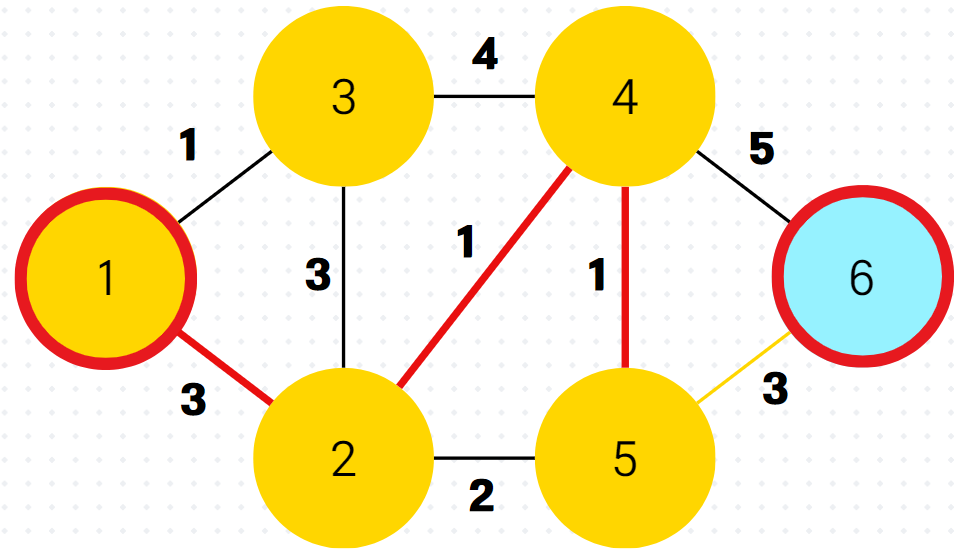
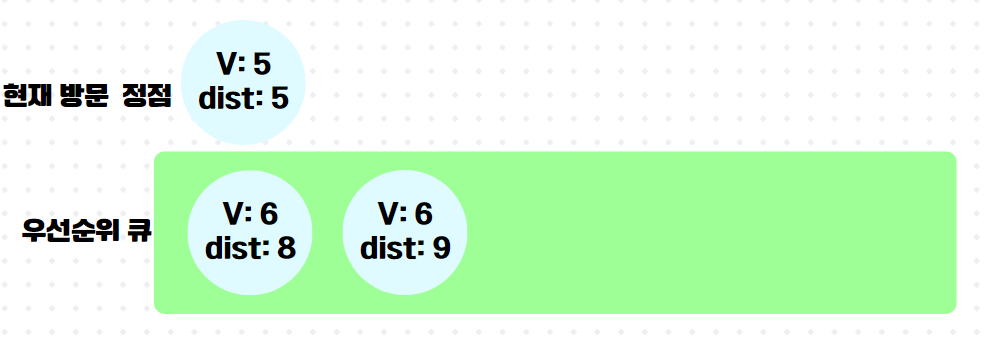
7.

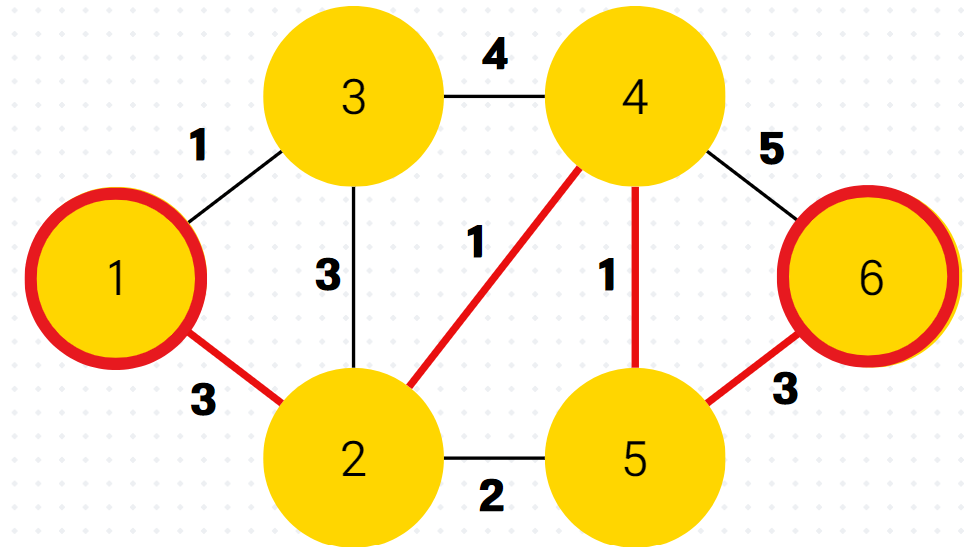
이후 남은 정점 속 dist 값도 최신화된 dist 배열(최단 거리 배열) 속 dist[6]보다 값이 크므로 그냥 PASS 한다.