1. 정의
양수인 가중치만 있는 그래프에서 시작점을 라고 할 때, 에서 모든 정점까지의 최단 경로를 구하는 알고리즘
최단 경로:
A ➜ B 의 최단경로는 A에서 B까지 가는 경로 중 최소 비용을 사용하는 경로를 의미한다.
가중치가 없는 그래프에서는 간선의 수가 적을수록 최단 경로가 될 것이고, 가중치가 있는 그래프에서는 가중치를 작게 사용할 수록 최단 경로가 될 것이다.
2. 원리
KEY WORD: GREEDY ALGORITHM
- 1️⃣ 시작점에서 각 노드까지 걸리는 최소 거리를 저장하는 배열을 만든다. (최소 거리 DASH-BOARD)
- 2️⃣ 현 시점에서 방문하지 않은 노드들 중, 시작점에서 가장 최소 비용으로 갈 수 있는 노드(이하 A)를 매번 고른다.
- 3️⃣ A와 인접한 노드들을 방문하고, 최소 거리 DASH-BOARD를 더욱 최소값으로 갱신할 수 있다면 갱신한다.
- 4️⃣ 위 과정을 모든 노드를 방문할 때 까지 반복한다.
과정 (2)에서 쓰인 것이 곧 GREEDY ALGORITHM이다. 매번 최소 비용으로 방문 가능한 노드를 방문하는 것이 종국에 모든 노드까지의 최소 비용을 구하게 해준다. 왜 이것이 가능할까? 계속해서 설명하겠다.
(1) BFS로는 가중치 있는 그래프에서 최단 경로를 구하지 못하는 이유
BFS는
- 1️⃣ 시작점을 deque에 넣는다. 이제 deque가 빌 때까지 밑의 과정을 반복한다.
- 2️⃣ deque의 front 값을 빼낸다. 해당 노드와 인접한 노드들을 차례로 확인한다.
- 2️⃣-1 만약 방문하지 않은 노드라면 deque에 넣는다.
(이제 deque에 넣은 노드는 방문 예정임으로 방문 여부 배열에서 true로 값을 바꾼다.)
- 2️⃣-1 만약 방문하지 않은 노드라면 deque에 넣는다.
- 3️⃣ 모든 노드를 방문할 때까지 과정 2️⃣를 반복한다.
의 과정으로 이루어진다.
해당 방식은 가중치가 없을때는 시작점에서 가까운 순으로 노드를 방문하므로, 최단 거리가 보장된다.
하지만 가중치가 있을 경우, 경유지 방문에 최소 비용을 소모했다는 것을 확신할 수 없기에 도착지까지 최소 비용을 썼다는 것을 확신할 수 없게 된다. 따라서 최단 경로를 구하지 못한다.

BFS로 푼다면, 위 그래프에서 맨 처음 B를 선택하고, B에 인접한 도착지를 deque에 넣음으로써, 계산이 종료될 것이다. 이 경우, BFS가 답한 도착지까지의 최소 비용은 6이다. 하지만,
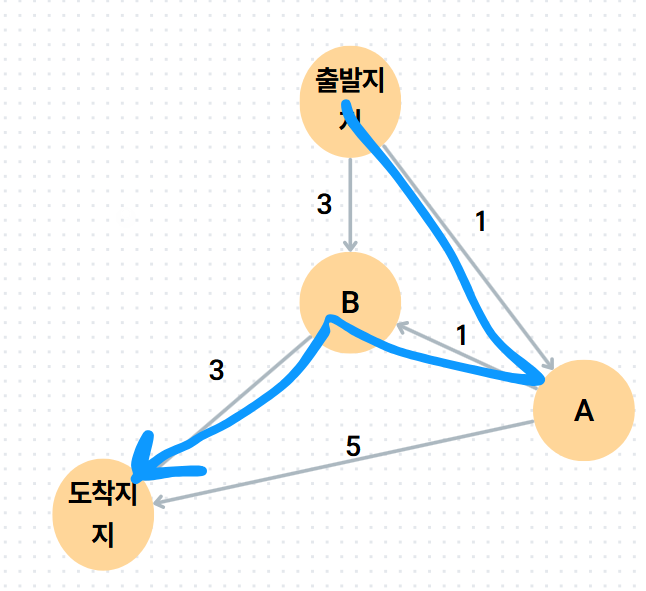
출발지➜A➜B➜도착지가 비용이 5임으로, 해당 BFS의 답은 정답이 아니다. 하지만 BFS는 이미 B를 방문해버렸기에 A ➜ B로 갈 수가 없게 된다. 따라서 정답을 구하지 못한다.
(2) GREEDY를 사용하면 경유지까지의 최단 거리도 보장됨
우리는 Greedy 알고리즘을 활용해 현 시점, 시작점에서 최소 비용으로 갈 수 있는 노드를 매번 고른다. 이러면 매번 최소 비용으로 갈 수 있는 경유지를 고르게 되어 맨 마지막 계산은 최소 비용으로 갈 수 있는 경유지가 곧 도착지가 되어 문제를 풀 수 있는 것이다.
이미 방문한 노드를 나중에 더 최소 비용으로 갈 수 있는 경우는 없을까? ✨
다익스트라의 조건 처럼 모든 가중치가 양수라면 그런 경우는 없다.
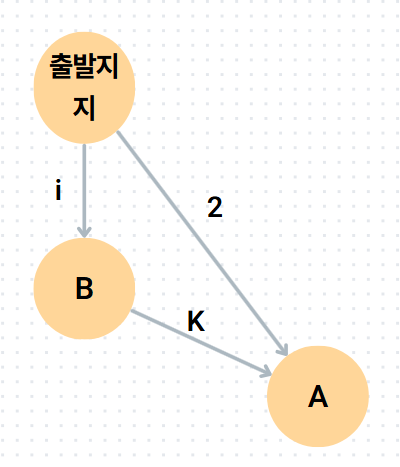
만약 출발지에서 방문할 노드로 A를 골랐다면 우리는 2 < i 임을 알 수 있다. 왜냐하면 다익스트라를 사용한다면 지금 갈 수 있는 노드 중 최소 비용 노드를 골랐을 것이기 때문이다.
이미 2보다 i가 큰데 K를 더한다고 해서, i+K < 2가 될 수 있는가? 불가능하다. 왜냐하면 K > 0임이 보장되기 때문이다.
따라서 GREEDY ALGORITHM을 활용하면 매번 최단 경로 경유지를 고를 수 있게 된다. 이는 시작점에서 각 경유지까지의 최단 거리도 구할 수 있게 되는 것임으로, 결국 시작점에서 모든 정점까지의 최단거리를 구하는 것과 마찬가지가 된다.
3. 구현
(0) 구성 요소
- : 시작점
dist []: index = 노드 번호, value = 에서 index 번호의 노드까지 최단 경로 비용을 저장(예를 들어, dist[5]는 시작점에서 노드 5까지 가는 최단 경로 비용을 저장하고 있다.)
(1) 구현 과정
- a. 를 선정한다.
- b. 현 시점에서 dist[]를 봤을 때, 방문하지 않은 노드 중 에서 최소 비용으로 갈 수 있는 노드를 선택한다. (이를 노드
A라 하겠다.) - c.
A와 인접한 노드들을 모두 확인한다. - d.
A와 인접한 노드 중 하나를B라고 해보자,- d-1.
dist[B]>dist[A] + A ➜ B의 비용: dist[B]를 dist[A] + A ➜ B 비용으로 최신화 - d-2.
dist[B]<=dist[A] + A ➜ B의 비용: 그냥 넘어간다.
- d-1.
- e. 과정
b에서 모든 노드를 방문할 때까지 b ∿ d까지의 과정을 반복한다.
dist [] 초기화 필수✨
계산을 위해서 dist의 모든 원소는 INF(간선 가중치 중 최대값 + 1), 시작점은 0으로 갱신해야 한다.
왜냐하면, 배열의 기본 초기화 값은 0임으로, 항상 그때 그때 dist[] 중 최소값을 골라 사용해야하는 다익스트라의 계산에 방해가 된다. 또한 시작점은 0으로 두어서 항상 최초로 선택하는 dist 최소값이 될 수 있도록 조치해야 한다.
과정 d-1에 대한 해설 ✨
dist[B] > dist[A] + A ➜ B의 비용의 의미는 '현재까지 알고 있던 $v\{start}$에서 노드 B까지의 최소 비용보다, 에서 *노드 A를 경유해 B로 가는 비용이 더 작다.*'_는 의미이다.

4. 예시

다음과 같은 그래프에서 다익스트라 알고리즘을 쓴다고 가정해보자. 시작 노드는 1이고, 우리가 값을 얻고 싶은 목표 노드는 6이다.


시작 노드에 대해서 거리 방문 처리 및 거리 배열의 값을 0으로 세팅한다. (예시에서는 노란색으로 색칠을 방문으로 간주한다.)


다음과 같이 1번의 인접 노드인 2,3이 값을 최신화 한다. 방문하지 않은 노드 중에 가장 거리 배열 값이 작은 (시작 노드에서 갈 수 있는 최단 경로인) 값은 무엇인가? 답은 노드 3이다.
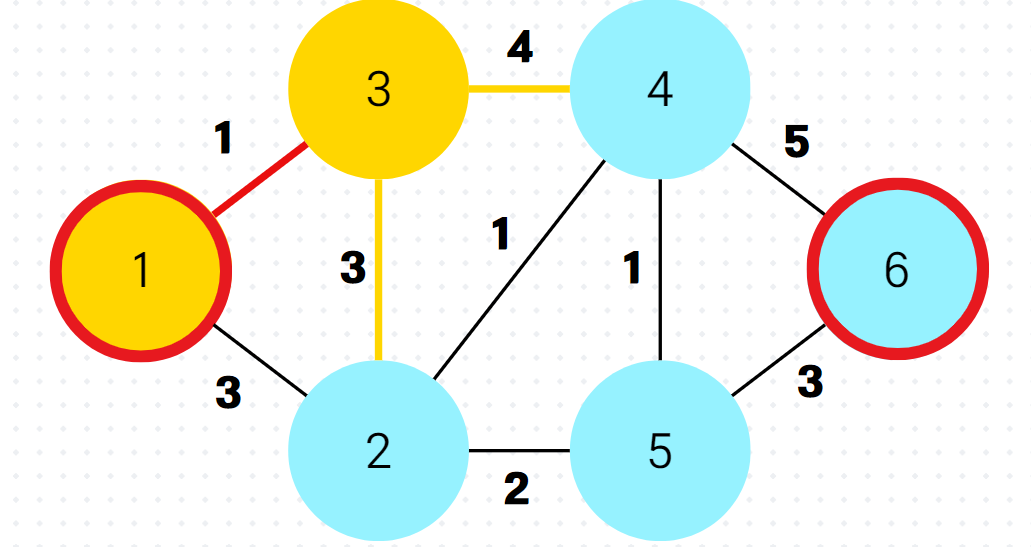
그럼 이제 3의 입장에서 거리배열을 갱신해보자. 방문 노드 제외하고 3에서 갈 수 있는 노드들은 2와 4번 노드이다.
2번의 경우를 생각해보면, 1 ➜2 와 1➜3➜2 중 최단 거리가 더 짧은 비용을 택하게 될 것이다.

2번 노드는 원래의 3이란 값이 더 최소값이라서 현행유지 할 것이다. 다음으로 1,3을 제외한 노드 중 시작 노드에서 가장 최단으로 갈 수 있는 노드는 2번임으로 2번을 선택한다.


방문하지 않는 노드들에 대한 갱신을 해보면, 4번 노드는 이전의 경로보다 현재 2번 노드를 통한 경로가 최단 경로라 갱신되는 것을 볼 수 있다. (2에서 3번 노드를 갱신하려고 해도, 최단 경로가 안되므로 갱신할 필요가 없다. - 이미 방문한 노드들은 방문 후 절대 값이 갱신 되지 않는다! 그 이유는 다음 장에서 설명하겠다.)


이제 그림으로만 진행하겠다.




도착 정점 방문을 마치는 순간 다익스트라 알고리즘은 끝난다. 1➜6 최단 경로 비용은 8이다.






