1. 문제 설명

2차원 배열의 값을 집어넣고, 그것을 1차원 배열로 늘어뜨려서, 문제에서 원하는 구간 내의 숫자들을 묶어서 반환하는 문제이다.

2. 접근 방식

KEY WORD: Brute Force, 1차원 배열과 2차원 배열의 위치 관계

해당 문제는 n의 maximum이 10^7이므로, O(n)을 초과하는 시간 복잡도를 사용하지 못한다. 따라서 2차원 배열에 값을 다 집어넣고, 그것을 1차원으로 만드는, 마치 문제에서 지시한대로는 풀이를 하지 못한다. 또한 1차원 배열을 바로 만들더라도, n*n은 배열의 메모리를 초과하는 값을 초래할 수 있기 때문에 1차원 배열 전체를 만드는 것도 무리다.
따라서 우리는 정확히 left ~ right 까지의 배열을 만들어 값을 구해 반환해야 한다.

(1) 1차원 배열 <-> 2차원 배열 올바르게 변환

(step 1) 1차원의 index를 통해, 해당 index의 원소가 2차원 배열이었다면 있어야할 위치를 구하고,
(step 2) 그 위치의 값을 구하는
2가지 절차를 거쳐야 한다.

그를 위해서 일단 배열의 모습을 보자.

문제에서 2차원을 1차원으로 바꾸는 방식은 단순하게, 1차원 배열을 처음부터 일렬로 배열하는 것이다.
따라서 (0,0) -> 0, (0,1) -> 1 ... (1,1) -> 4 ... (2,2) -> 8 임을 알 수 있다. 이 둘 사이를 변환하는 공식을 작성해보면 다음과 같다.

(x,y) -> Z // x,y = 2차원 배열의 행렬 값, Z = 1차원 배열에서의 index
 x*n + y = Z

따라서 1차원 배열의 index Z 입장에서 볼 때, x는 n으로 나누었을 때 몫이고 y는 n으로 나누었을 때 나머지임을 알 수 있다. 이걸 이용해서 1차원 배열의 각 index에 맞는 2차원에서의 위치를 찾을 수 있다.

이제 step2를 해보자. 2차원 배열의 index를 통해 거기에 해당하는 값을 찾는 것이다.

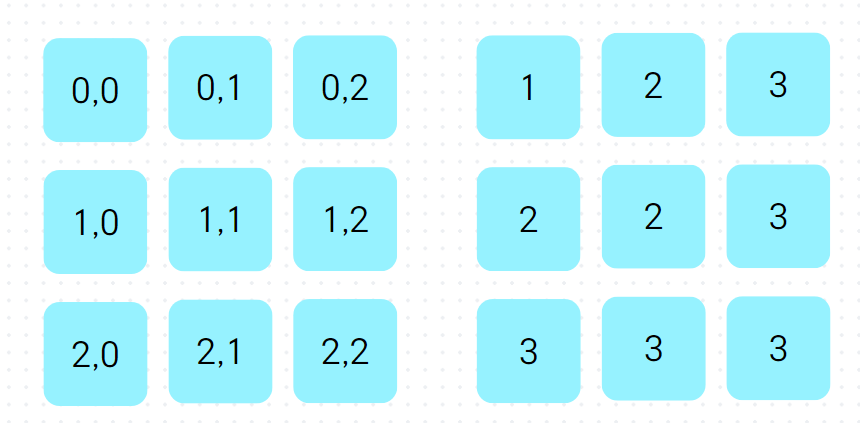
둘 간의 관계를 보면 Math.max(x,y) + 1 == arr[x][y]임을 알 수 있다. 이를 통해 2차원 배열 각 원소를 구한다.

나머지는 간단하다. 이 두 가지 원리를 가지고 1차원 배열에서 index == left 부터, == right 까지의 값들만 구해서 반환하면, 된다.

3. 코드 풀이

import java.io.*;
import java.util.*;

class Solution {
    /*
        n의 maximum이 10^7이므로, O(n)안에 처리 해야 한다.
        1. 1차원 배열을 만든다. 
        2. 1차원 배열의 인덱스를 2차원 배열로 변환한다. (n으로 나눈 몫, n으로 나눈 나머지)
        3. 2차원일때 인덱스를 통해 값을 집어 넣는다. 
        4. 배열을 잘라서 반환한다.

    */ 
    public int[] solution(int n, long left, long right) {  
        int [] ans = new int [(int)(right-left+1)];
        int start = 0;
        for(long i = left; i <= right; i++){
            ans[start++] = Math.max((int)(i/n), (int)(i%n)) + 1;
        }
        return ans;
    }
}

4. 성장 하기

import java.io.*;
import java.util.*;

class Solution {
    /*
        n의 maximum이 10^7이므로, O(n)안에 처리 해야 한다.
        1. 1차원 배열을 만든다. 
        2. 1차원 배열의 인덱스를 2차원 배열로 변환한다. (n으로 나눈 몫, n으로 나눈 나머지)
        3. 2차원일때 인덱스를 통해 값을 집어 넣는다. 
        4. 배열을 잘라서 반환한다.

    */ 
    public int[] solution(int n, long left, long right) {  
        int [] ans = new int [(int)(right-left+1)];
        int start = 0;
        for(int i = (int)left; i <= (int)right; i++){
            ans[start++] = Math.max((int)(i/n), (int)(i%n)) + 1;
        }
        return ans;
    }
}

내 첫 풀이인데, 55점 맞고 계속 틀렸었다. 아이디어에 문제가 있는가 싶어서 한참 찾아봤지만 문제는 정작 다른 곳에 있었다. 문제는 바로, casting과 관련된 것이었다. n의 최대 크기가 10^7 이 될 수 있으니 n*n은 2.10 x 10^9 인 int 최대형 안에 다 담을 수 없는데, 위의 풀이를 보면, for문을 int 형으로 돌고 있다. 만약, left나 right가 이미 int형의 최대치를 넘어섰다면, for문을 도는 과정에서 이미 오버플로우가 나서 오류를 일으킨다.
따라서, for문은 left와 right 구간의 값들이 충분히 표현될 수 있게, long으로 돌고, ans에 넣는 값들은 n으로 나눈 것이니, 충분히 int안의 값으로 표현될 수 있으므로, 몫이나 나머지를 구한 후 그 값을 int형으로 캐스팅 해주는 게 필요하다.

casting에 대해서 크게 신경 안 쓰고 자주 넘어갔는데, 해당 문제는 큰 교훈을 준 것 같다.