하나 또는 다수의 소수 판별법, 그림으로 쉽게 이해하기

1. 하나의 숫자에 대한 소수 판별

(1) 방법

만약 소수인지 판별해야할 숫자를 N이라고 한다면, 다음과 같은 방법으로 N이 소수인지 여부를 판별할 수 있다.

int N = Integer.parseInt(br.readLine());

for(int i = 2; i<= Math.sqrt(N); i++){
    if(N%i == 0) System.out.println("소수가 아닙니다.");
    return;
}
// 2이상 √N이하의 모든 수에 대해서 나누어 떨어지지 않았다면, 
System.out.println("소수 입니다.");

(2) 왜 √N까지만 확인하면 되나요?

'N에게 약수가 존재한다면, 약수는 곱해서 N을 만들 수 있는 각자의 짝이 존재한다. 짝이 되는 약수의 쌍을 (A,B)라 할 때, A가 √N보다 작다면, B는 √N보다 크다.'

위의 성질을 이용해서, √N의 이하만 확인한다. 만약 √N 이하인 부분에서 1을 제외한 어떠한 수도 N을 나눌 수 없다면, √N 이상의 반대편에서도 N 자신을 제외한 어떤 수도 N을 나눌 수 없음이 증명된다. 따라서 N은 소수임이 판명된다.

예시 🧩

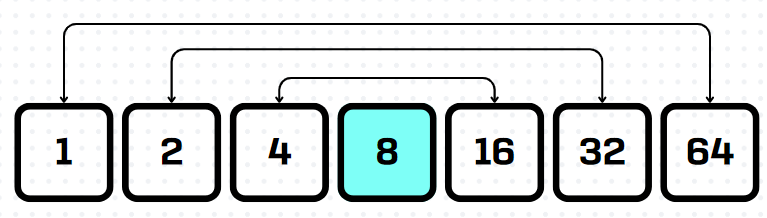
N = 64, √N = 8이라 할 때,

N을 나눌 수 있는 약수를 찾는 문제라고 가정하자. √N인 8 이하에서 N을 나눌 수 있는 값 [1,2,4,8]을 찾았다면, 그것으로 나눌 때의 몫 [64,32,16,8]도 자동으로 찾아진다. 따라서 N의 모든 약수를 찾을 때도 √N 이하만 보면 된다.

N = 17, √N = √17

같은 원리로 소수인지 판별을 위해서도 √N 이하만 보고, 나누어지는 값이 1빼고 아무것도 없다고만 확인하면 된다.

2. 특정 범위 내의 숫자들에 대한 소수 판별

KEY WORD: 에라토스테네스의 체

특정 영역에 소수를 전부 알고 싶을 때, 첫 번째 방법처럼 모든 수에 대해서 일일히 소수 판별을 거치는 것은 매우 비효율적이다. 아마 시간 복잡도는 $O(N \sqrt{N})$ 가 들 것이다.

따라서 영역 내 모든 수에 대한 소수 판별 접근 방식을 일일히 전부 다 하기에서 한 번에 다하고, 필요할 때마다 꺼내 쓰기로 바꿀 필요가 있다.

(1) 에라토스테네스의 체란?

체로 불순물을 걸러내듯이, 소수가 아닌 값들을 차례로 걸러내며, 영역 내에 소수만 남기는 방식이다.

(2) 과정

• 0️⃣ index = 숫자, value = 소수면 true, 아니면 false인 1차원 배열(이하 arr)을 소수 판별이 필요한 영역 만큼 만든다.
• 1️⃣ 2부터 시작해서 오름차순으로 수를 조회한다.
  • (1️⃣-1) 만약 현재 조회 중인 수를 i라 할 때, arr[i] = true이면, 영역 끝까지, index가 i의 배수인 모든 arr값을 false로 바꾼다. (현재 조회한 값은 그대로 true로 놔둠)
  • (1️⃣-2) arr[i] = false이면 넘어간다.
• 2️⃣ 1번의 과정으로 체가 전부 걸러졌다. 이제 문제에서 원하는 나머지 계산을 하면 된다.

출처: 위키피디아 에라토스테네스의 체

(3) 구현

int N = Integer.parseInt(br.readLine);
boolean [] isPrime = new boolean [N + 1];

// default 값 true로 바꾸기
for(int i = 0; i< isPrime.length; i++){
    isPrime[i] = true;
}

// 소수 판별 -> 소수가 아닌 값들은 false로 바뀐다.
for(int i = 2; i<= Math.sqrt(N); i++){
    if(isPrime[i]){
        for(int j = i*i; j <= N; j += i){
            // 소수의 배수들은 모두 false 처리
            isPrime[j] = false;
        }
    }
}

소수 판별에서 i를 √N까지만 봐도 되는 이유? 🧐

결론 : 모든 소수 K는 영역 내에서 K*K를 시작으로 자신의 배수를 지우기에, √N을 초과한 소수는 자신이 지울 배수가 영역안에 없어서 안 봐도 된다.

바깥 반복문에서, 소수 K를 만났다고 치자. 그렇다면, 소수 K는 K * K부터 시작해서 자신의 배수를 지워나간다. 왜냐하면 K * K 이전의 K의 배수들은 이미 K보다 작은 소수들이 전부 지워놨기 때문이다.

예를 들어, 소수 5는 25부터 시작해서 자신의 배수를 지워나간다. 그 이전에 있었던 10과 15는 이미, 2,3이 자신의 배수를 처리할 때, 처리 했다. 같은 의미로 N = 121 이라면, 11은 영역안에서 자신이 지울 숫자가 없다. 자신의 배수는 11이하의 소수 2,3,5,7이 전부 지웠기 때문이다.

√N이 소수일 경우, 그것이 지워야할 자신의 첫 번째 배수가 N이 되므로, √N 을 초과한 소수들은 영역 내에 자신의 배수가 없다는 것이다. 따라서 안 구해도 된다.

(4) 시간복잡도

범위를 1 ~ N까지라 봤을 때, 에라토스테네스의 체 구현을 이중 반복문으로 해서 시간 복잡도가 $O(N^{2})$라고 생각할 수 있지만, '이미 소수가 아니다.'(false)라고 정해진 수는 다시 들여다 보지 않고, 넘어감으로, 실제 시간 복잡도는 $O(N \log(\log N))$ 이다.