벨만 포드 알고리즘, 그림으로 쉽게 이해하기

1. 벨만포드 알고리즘이란?

음수인 가중치가 존재하는 그래프에서도 최단 경로를 구할 수 있게 해주는 알고리즘.

• ONE TO ALL 알고리즘: 시작점을 고르면, 해당 정점에서 모든 정점까지의 최단 경로를 구할 수 있다.
• 다익스트라와 달리, 음수 가중치가 있어도 최단 경로 구할 수 있다.
• 음수 사이클이 존재하는지도 확인 가능: 음수 사이클이 존재한다면, 사실 하나 이상의 정점으로의 최단 경로가 $- \infin$가 되기 때문에, 최단경로를 구하는 게 무의미해짐. 따라서 최단 경로를 구하는 게 무의미한지 여부도 파악 가능!

음수 사이클

가중치 그래프에서 정점 A에서 시작해서 A로 돌아왔는데 가중치의 합이 음수인 경우, 해당 사이클을 음수 사이클이라고 한다.

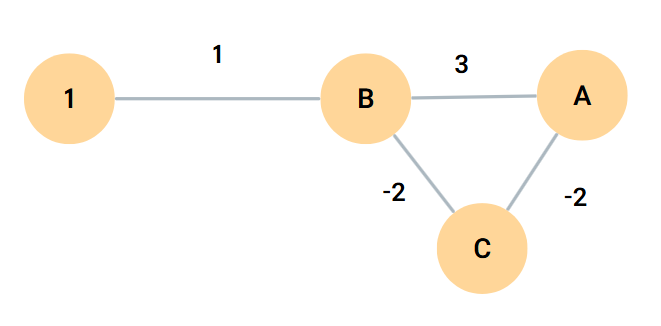
해당 예시에서는 사이클을 돌수록 출발지에서 A,B,C까지의 거리가 짧아진다. 따라서 최단경로를 구하는 것의 의미가 없다.

2. 벨만포드의 과정

정점의 수를 V, 간선의 수를 E라고 하자.

• 0️⃣ 사전 세팅
  • 시작 정점 정하기
  • 최단 거리 배열(이하 dist) 만들기 (index = 도착정점, value = 시작 정점에서 해당 정점까지의 최단 거리)
  • 그래프를 간선리스트로 구현하기 <출발 정점, 도착 정점, 간선 가중치>
• 1️⃣ $V-1$ 번 돌면서, 모든 간선에 대하여 다음을 반복한다.
  • 현재 보고 있는 간선의 정보를 <start=A, end=B, weight=C>라고 해보자.
  • 만약 dist[A] = $\infty$ 이면 바로 다른 간선으로 넘어간다.
  • dist[A] $\neq \infty$ 일 시, dists[B] > dist[A] + C를 성립한다면, dist[B]를 dist[A] + C로 갱신한다. (이 갱신 과정을 완화라고 부른다.)
• 2️⃣ 마지막으로 한 번 더 1️⃣을 수행해본다. 이후 간선의 가중치가 더 작아진 녀석이 하나라도 존재하면, 해당 그래프에는 음수 사이클이 존재한다는 의미이다.

(1) 1️⃣을 V-1번만 반복하는 이유

정점의 수를 V개라 할 때, 임의의 정점 A에서 B로 가는 경로 안에 존재할 수 있는 간선의 최대 개수는 V-1개 이다.

벨만포드 알고리즘은 한 번의 반복에서 최소 하나의 간선을 더 활용하여, 유의미한 비용 완화를 일으킨다. 따라서, 모든 간선을 활용한 완화가 일어나서 최종적으로 모든 정점에 가는 최단거리를 구하기 위해서는 V-1번의 반복이 필요한 것이다.
V번째 반복부터는 음수 사이클이 없는 한 최단 거리 감소가 일어나지 않는다. 왜냐하면 이미 모든 간선을 활용하여 최단거리 계산을 마쳤기 때문이다.

 

(2) 사실 최단거리 계산은 V-1 이전에 끝날 수 있다.

V-1번 반복이 최단 거리를 확실히 구하는 최소 조건일 뿐이지, 최단 거리 계산은 V-1번 이전에 끝날 수 도 있다. 예를 들어 다음과 같이 그래프가 존재한다고 해보자.

A를 출발지점이라 할 떄, dist[] 배열은 [0, 무한대, 무한대] 일 것이다. 입력이 (출발 정점, 도착 정점, 가중치) 형태일 때, 역순으로 들어왔다고 치면, (B, C, -1), (A, B, -1) 일 것이다. 이대로 완화를 진행 한다면,

• 먼저 첫번째 반복에서, B가 무한대이기 때문에 첫번째 간선 리스트는 의미가 없다. 따라서 이후 (A,B,-1)만 가중치 완화에 사용된다. 결과: [0, -1, 무한대]
• 두번째 반복에서는 첫번째 간선을 활용할 수 있어 최종적으로 다음과 같이 완화될 것이다. 결과: [0, -1, -2] 이는 N-1번인 2번 안에 결과가 나온 것이다.

그런데 만약 입력이 (A, B, -1), (B, C, -1)로 반대로 들어왔다면 어떻게 될까?

• 첫 번쨰 반복에서 먼저 (A, B, -1)에 따라 거리 배열이 완화된다. [0,-1,무한대] 이후 바로 다음 간선 리스트로 한 번의 반복에서 최단거리 배열 계산이 끝난다. [0,-1,-2]

위와 같이 V-1은 벨만 포드를 완성시키기 위한 최소 조건이지, 그 이전에 최단거리 계산이 끝날 수 있다. 따라서 저번 반복과 비교하여 완화된 최단거리가 없다면 탈출해도 될 것 같다.

(3) 그림으로 이해하기✨

벨만포드는 한번의 반복마다, 간선이 점진적으로 사용되며, 완화되는 과정을 보는 것이 중요한데, 그림으로 하나하나 그리기가 귀찮아서 생략하겠다. 해당 그림을 정말 잘 표현하신 블로그를 동봉드리니, 독자분들은 한 번보고 오시길 바란다.
Link

[Algorithm] 벨만-포드 (Bellman-Ford) 알고리즘

 

3. 시간 복잡도

정점의 개수를 $V$, 간선의 개수를 $E$ 라고 할 때, 모든 간선을 V번 돌아야 한다. 따라서 시간복잡도는
$$O(VE)$$
이다.

4. 벨만포드의 구현

시작 정점이 모인 배열을 a[], 도착 정점이 모인 배열을 b [], 간선이 모인 배열을 c []라고 할 때, i 번째 값들은 하나의 간선을 나타낸다고 하자. 즉 a[i],b[i],c[i]는 a[i]에서 b[i]로 가는 가중치가 c[i]인 간선이다.

간선의 개수를 M개라고 할 때,

public class Main {    
    static int [] a, b;
    static long [ ] c, dist;
    public static void main(String[] args) throws IOException { 
        for (int i = 0; i < M; i++) {
            int start   = a[i];
            int end     = b[i];
            long weight  = c[i];
            long oldValue = dist[end];

            if(dist[start] != Long.MAX_VALUE){
                dist[end] = Math.min(dist[end], dist[start] + weight);
            }

            if(oldValue != dist[end]){
                System.out.println(-1);
                return;
            }
        }
    }
}

M-1번째 반복까지는 dist[]의 값을 계속 완화시켜 작게 갱신한다. 이후 M번째 반복에서는 하나의 최단 거리 값이라도, 완화 과정을 거쳤더니, 값이 갱신되면 음수 사이클이 있는 것임으로, 해당 그래프는 최단 거리 계산이 불가하다는 의미의 -1을 출력했다.